Comet OJ – Contest #9 & X Round 3 题解
Visits: 1249
【XR-3】等差数列
by xht37 & NaCly_Fish
前置知识
- 模拟或等差数列求和
方法一
因为一共只有 $n \le 10^6$ 项,所以可以把数列的每一项都求出来然后相加即可,时间复杂度 $\Theta(n)$。
方法二
根据前两项的值算出公差,就可以求出第 $n$ 项,然后用等差数列求和公式 $S=\frac{(a_1+a_n)n}{2}$ 计算即可,时间复杂度 $\Theta(1)$。
【XR-3】小道消息
by meaningful & NaCly_Fish
前置知识
- 简单数论
本题题解
如果 $k + 1$ 是质数且 $2(k+1)>n+1$,则答案为 $1$,因为它一定与 $2 \sim n+1$ 的数(除了自己本身)互质。
否则答案为 $2$,因为根据伯特兰-切比雪夫定理,$k+1$ 一定与 $2 \sim n+1$ 中最大的质数互质,因此第一天衣服上写有这个最大质数的人一定会得到这条小道消息,那么在第二天所有人都会知道。
时间复杂度即为判断质数的时间复杂度,$\Theta(\sqrt n)$ 即可。
【XR-3】核心城市
by meaningful
前置知识
- 树的直径与树的中心
- 堆
本题题解
如果 $k =1$,则唯一的核心城市显然为树的中心(若直径上有偶数个点,则任意选择中间两个点中的一个)。
当 $k \ne 1$,我们可以把树的中心当成根,然后我们依次将点贪心地加入核心城市中。
定义 $f_x$ 为以树的中心为根时,点 $x$ 离自己子树中的叶子的最大距离。
那么,我们可以每次在与当前确定的核心城市相连的非核心城市中选择 $f$ 最大的城市加入到核心城市中,直到核心城市的数量到 $k$ 为止。这可以用堆实现,时间复杂度 $\Theta(n \log n)$。
【XR-3】系统设计
by PinkRabbit
前置知识
- 字符串 Hash
- 树状数组/线段树上二分
本题题解
将树上根到节点 $u$ 的简单路径依次经过的边的排名记作一个字符串 $s_u$。
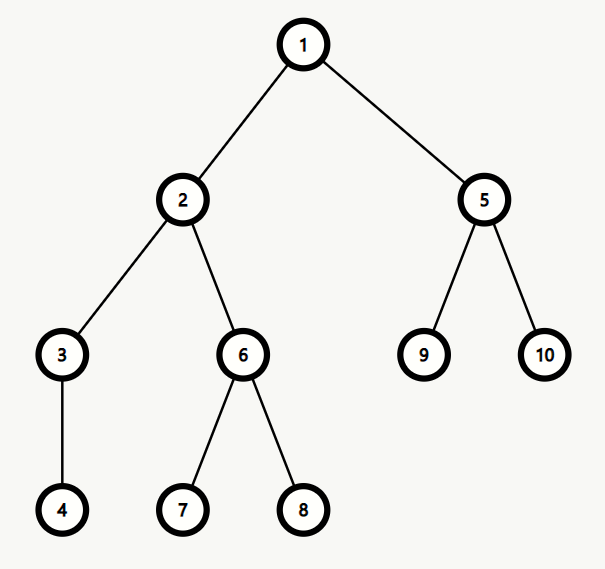
例如上图中,有:
$$
\begin{aligned}
s_1&=\texttt{“”}(空串)\\
s_2&=\texttt{“1”}\\
s_3&=\texttt{“11”}\\
s_4&=\texttt{“111”}\\
s_5&=\texttt{“2”}\\
s_6&=\texttt{“12”}\\
s_7&=\texttt{“121”}\\
s_8&=\texttt{“122”}\\
s_9&=\texttt{“21”}\\
s_{10}&=\texttt{“22”}\\
\end{aligned}
$$
考虑询问 1 x l r 时,将 $a_{l..r}$ 也看作一个字符串,并在前面拼上 $s_x$ 这个字符串。
则转化为查询 $str=s_x+a_{l..r}$ 在树中最长能够匹配到哪个点。
举个例子,若 $x=2,a_{l..r}=\texttt{“231”}$,则 $str=s_2+a_{l..r}=\texttt{“1231”}$。
最长能匹配上 $s_6=\texttt{“12”}$,则答案为 $6$。
考虑字符串哈希,预先处理所有节点表示的字符串的哈希值,并存在哈希表里。
用数据结构维护序列的哈希值,查询时在数据结构上二分,在哈希表中查询是否存在此值即可。
时间复杂度 $\Theta((n+(m+q)\log m)\times T(\mathrm{hash}))$。
【XR-3】Namid[A]me
by EntropyIncreaser
首先介绍如何快速计算 $x^x \bmod P$。注意到模数 $P = 786433$ 非常小,且在题目中给出了模数的一个原根,因此我们可以轻松在 $\Theta(P)$ 的时间内预处理出 $1 \sim P – 1$ 每个数的离散对数 $ind[x]$ 以及幂 $pow[k] = g^k \bmod P$。通过欧拉定理即可在 $\Theta(1)$ 时间内计算 $x^x = pow[ind[x] x \bmod (P – 1)]$。需要特判 $x \equiv 0 \pmod P$ 的情况。
接下来考虑一条链如何计算。
这样所有链都等价于一个区间,考虑枚举右端 $r$,那么对于 $[l, r]$ 内所有数的与设为 $x_l$,注意到若 $x_l \neq x_{l + 1}$,由于 $x_l = x_{l+1} \operatorname{\texttt{and}} a_l$,那么必然是至少在 $x_{l+1}$ 中的一个二进制位从 $\texttt{1}$ 变为 $\texttt{0}$。因此,从 $x_l$ 到 $x_1$,必然最多只有 $w + 1$ 种取值。我们考虑只维护被取到的值分别取到了多少次即可。
接下来注意对于一个有 $d$ 个叶子的子树,在维护时子树内每个节点到子树的根的路径上的与和总共不超过 $d(w+1)$ 种取值,这是因为将每个叶子到根的一条链内的取值各自都不超过 $w + 1$。我们只需在 DFS 的过程中维护每个子树内所有能取到的值的出现次数即可。这一部分的复杂度为 $\Theta(ndw)$。在处理子树的时候,我们还需计算路径两端点在不同子树的路径的答案,这一部分我们暴力枚举,注意到两个叶子只会在它们的 LCA 位置为合并的复杂度贡献 $(w+1)^2$,因此计算这一部分答案的总代价为 $\Theta((dw)^2)$。但是同时又有另一个显然的上界:$\Theta(n^2)$,因为只有这么多条路径,而在 $nd$ 总体有限制的这一条件下,考虑不等式 $\min(a, b) \le \sqrt{ab}$,可知这一部分的复杂度不超过 $\Theta(\min(n, dw) ^2) \le \Theta(ndw)$。
综上所述,本算法的复杂度为 $\Theta(ndw)$。
【XR-3】Unknown Mother-Goose
by Shadowice1984
题目的数据范围很具有迷惑性,可能会让人认为标算是 $\Theta(2^s)$ 的容斥,而 $n$ 只有 $10^9$ 则是为了避免解同余方程时爆 long long。
其实标算是 bitset 大暴力啦。
一个可能的暴力是:开一个长度是 $10^9$ 的布尔数组 $a$,把是 $S$ 中每一个元素的倍数的下标全部赋值成 $1$,那么,如果 $a_x,a_{x-1},a_{x+1}$ 都是 $1$,$x$ 就是合法的。
如果把暴力中的布尔数组用 bitset 存储,问题就变成了数 bitset 里有几组三个连续的 $1$,你可以通过一套 & 操作转化为数 popcount。
不过还可以每 $64$ 位分一块,块内算一下内部有几组三个连续的 $1$,然后算块和块之间有几组三个连续的 $1$,这个枚举一下即可。
这样的复杂度是 $\Theta(\frac{n}{8})$ 的,因为 popcount 的底层实现实际上是查 $65536$ 长度的表。
下面是如何生成这个 bitset,暴力并不清楚能不能过,因为可以去重,加上特判 $1$ 之后胡乱暴力。
为了跑的快点,你可以根据 $S$ 中的元素是否大于 $64$ 来分情况讨论 ,如果大于 $64$ 那么暴力的赋值,如果小于等于 $64$,每一块实际上被按位或的 01 串很快就会出现循环节,直接预处理出这些循环的 01 串,然后按位或即可。
总时间复杂度 $\Theta(\frac{n|S|}{64} + \frac{n}{8})$。
理论复杂度算起来很高,但是寻址连续并且不会频繁调用系统栈(对比大家平时写的算法),所以可以很快的通过。
顺便说一句,建议手写 bitset。


