Visits: 270

CF587D Duff in Mafia

题意

• 给定一张 $n$ 个点 $m$ 条边的无向图，每条边有一个颜色 $c$ 和权值 $t$。
• 你要选出一些边，使得它们是一个匹配，同时剩下的边每种颜色也是一个匹配。
• 同时，你要最小化选出的边的最大权值。
• $n,m \le 5 \times 10^4$。

题解

首先二分答案，若此时二分的值为 $o$，则所有 $> o$ 的边都不能选。

每条边有选和不选两种状态，所以考虑 2-SAT。设第 $i$ 条边的状态为 $x_i$ 表示选择它，$x^{\prime}_i$ 表示不选。连边如下：

1. 对于一定不能选的边，连边 $x_i \to x^{\prime}_ i$。
2. 对于选出的边一定要是一个匹配，考虑一个点 $p$ 上的所有边 $x_{1\dots k}$，连边 $x_i \to x^{\prime}_ j(i \ne j)$。
3. 对于剩下的边每种颜色也一定要是一个匹配，考虑一个点 $p$ 上颜色相同的所有边 $x_{1\dots k}$，连边 $x^{\prime}_ i \to x_j(i \ne j)$。

但这样做第 $2,3$ 类边的边数为 $\mathcal O(m^2)$，注意到 2-SAT 有一个经典的建图优化——前缀优化。

先考虑第 $2$ 类边，设 $x_{1\dots k}$ 的前缀点为 $s_{1\dots k}$，$x^{\prime}_ {1\dots k}$ 的后缀点为 $s^{\prime}_ {1\dots k}$。连边如下：

1. $x_i \to s_i$，$s^{\prime}_ i \to x^{\prime}_ i$。
2. $s_{i-1} \to s_i$，$s^{\prime}_ i \to s^{\prime}_ {i-1}$。
3. $s_{i-1} \to x^{\prime}_ i$，$x_i \to s^{\prime}_ {i-1}$。

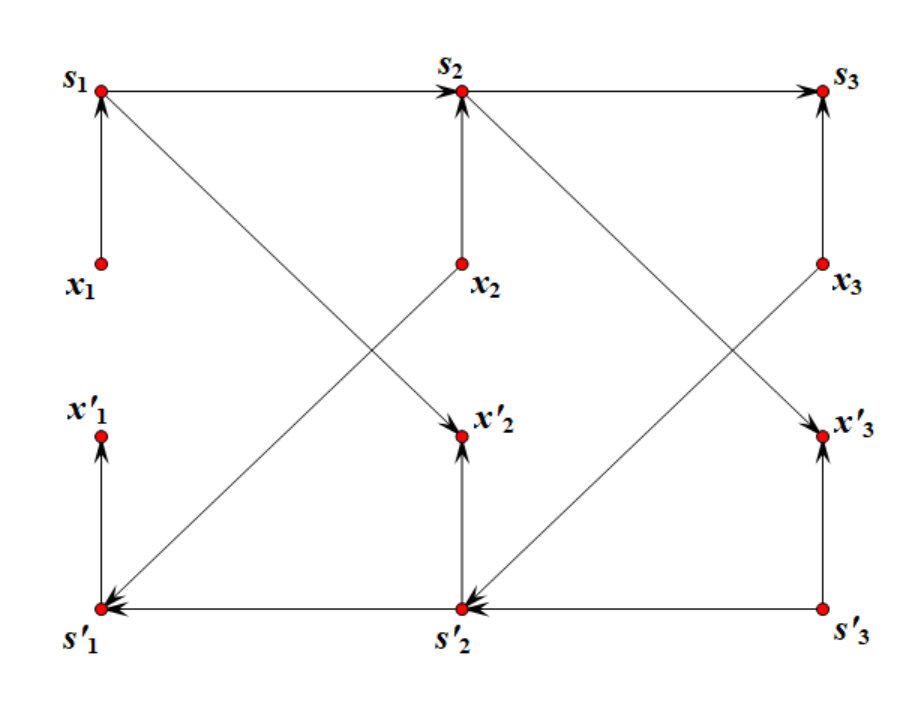
容易发现和第 $2$ 类边是等效的。

而第 $3$ 类边，就把第 $2$ 类边的箭头全部反过来即可。

然后 tarjan 就好了。

总时间复杂度 $\mathcal O((n + m) \log w)$。

代码

const int N = 5e4 + 7, M = 10 * N;
int n, m, tot, l, r;
int dfn[M], low[M], num, stk[M], top, ins[M], scc[M], cnt;
vi v[N], s, e[M], ans;
struct P {
    int u, v, c, t;
    inline void in() {  rd(u), rd(v), rd(c), rd(t), r = max(r, t); }
} p[N];

inline void work1() {
    int S, T;
    for (ui i = 0; i < s.size(); i++) {
        int x = ::s[i], y = ::s[i] + m, s = ++tot, t = ++tot;
        e[x].pb(s), e[t].pb(y);
        if (i) e[S].pb(s), e[t].pb(T), e[S].pb(y), e[x].pb(T);
        S = s, T = t;
    }
    s.clear();
}

inline void work2() {
    int S, T;
    for (ui i = 0; i < s.size(); i++) {
        int x = ::s[i], y = ::s[i] + m, s = ++tot, t = ++tot;
        e[s].pb(x), e[y].pb(t);
        if (i) e[s].pb(S), e[T].pb(t), e[y].pb(S), e[T].pb(x);
        S = s, T = t;
    }
    s.clear();
}

void tarjan(int x) {
    dfn[x] = low[x] = ++num, stk[++top] = x, ins[x] = 1;
    for (auto y : e[x])
        if (!dfn[y]) tarjan(y), low[x] = min(low[x], low[y]);
        else if (ins[y]) low[x] = min(low[x], dfn[y]);
    if (dfn[x] == low[x]) {
        ins[x] = 0, scc[x] = ++cnt;
        while (x != stk[top--]) {
            int y = stk[top+1];
            ins[y] = 0, scc[y] = cnt;
        }
    }
}

inline void init(int o) {
    for (int i = 1; i <= m; i++) if (p[i].t > o) e[i].pop_back();
}

inline bool pd(int o) {
    for (int i = 1; i <= m; i++) if (p[i].t > o) e[i].pb(i + m);
    for (int i = 1; i <= tot; i++) dfn[i] = 0;
    cnt = num = 0;
    for (int i = 1; i <= tot; i++) if (!dfn[i]) tarjan(i);
    for (int i = 1; i <= m; i++)
        if (scc[i] == scc[i+m]) return init(o), 0;
    return init(o), 1;
}

int main() {
    rd(n), rd(m), tot = m << 1;
    for (int i = 1; i <= m; i++)
        p[i].in(), v[p[i].u].pb(i), v[p[i].v].pb(i);
    for (int i = 1; i <= n; i++) {
        sort(v[i].begin(), v[i].end(),
            [&](int i, int j) { return p[i].c < p[j].c; });
        s = v[i], work1();
        for (ui l = 0, r = 0; l < v[i].size(); l = ++r) {
            s.pb(v[i][l]);
            while (r + 1 < v[i].size()
                && p[v[i][r+1]].c == p[v[i][r]].c) s.pb(v[i][++r]);
            work2();
        }
    }
    if (!pd(r)) return prints("No"), 0;
    prints("Yes");
    while (l < r) {
        int mid = (l + r) >> 1;
        if (pd(mid)) r = mid;
        else l = mid + 1;
    }
    pd(l);
    for (int i = 1; i <= m; i++) if (scc[i] < scc[i+m]) ans.pb(i);
    print(l, ' '), print(ans.size());
    for (auto x : ans) print(x, ' ');
    return 0;
}