Visits: 562

CF506E Mr. Kitayuta’s Gift

题意

• 给定一个小写字符串 $s$ 和一个正整数 $n$。
• 要求在 $s$ 中插入恰好 $n$ 个小写字符使其回文的方案数。
• $|s| \le 200$，$n \le 10^9$，答案对 $10^4 + 7$ 取模。

题解

首先考虑 $n+|s|$ 为偶数的情况。

考虑 dp。设 $f_{i,l,r}$ 表示只考虑最终回文串的前 $i$ 和后 $i$ 个字符，它们与 $s$ 尽可能匹配后 $s$ 还剩下 $[l,r]$ 这段区间时的方案数。再设 $g_i$ 表示只考虑最终回文串的前 $i$ 和后 $i$ 个字符，它们与 $s$ 已经能够完全匹配时的方案数。

那么转移有：

1. $s_l = s_r$，$r – l \le 1$。

$$
g_{i+1} \leftarrow f_{i,l,r}
$$

$$
f_{i+1,l,r} \leftarrow 25 \cdot f_{i,l,r}
$$

2. $s_l = s_r$，$r – l \ge 2$。

$$
f_{i+1,l+1,r-1} \leftarrow f_{i,l,r}
$$

$$
f_{i+1,l,r} \leftarrow 25 \cdot f_{i,l,r}
$$

3. $s_l \ne s_r$。

$$
f_{i+1,l+1,r} \leftarrow f_{i,l,r}
$$

$$
f_{i+1,l,r-1} \leftarrow f_{i,l,r}
$$

$$
f_{i+1,l,r} \leftarrow 24 \cdot f_{i,l,r}
$$

4. $g$。

$$
g_{i+1} \leftarrow g_i
$$

此时我们可以得到一个状态数 $\mathcal O(|s|^2)$ 递推 $\mathcal O(n + |s|)$ 次的 dp，这个 dp 可以强行矩阵加速，复杂度为 $\mathcal O(|s|^6 \log (n + |s|))$，一脸的过不去。

仔细观察这个 dp，可以发现这实际上是在一个有限状态自动机上匹配的过程。

比如对于 $s = \texttt{abaac}$ 转移的过程如下：

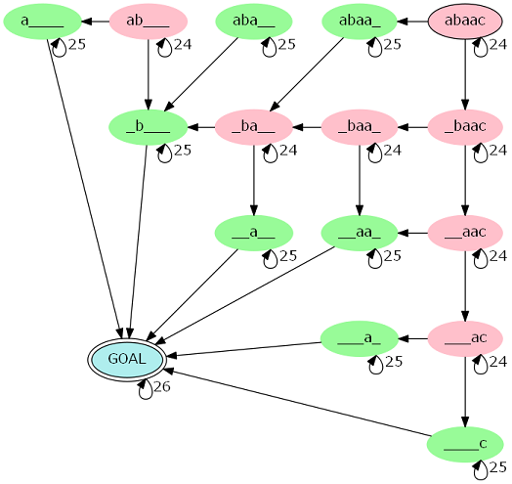
如果真的理解了上面的 dp，会发现这张图中不同颜色的点和不同形态的边与上面的状态和转移一一对应。

这个自动机的节点数依旧是 $\mathcal O(|s|^2)$ 的。考虑压缩这个自动机，可以发现，对于每一条从起点到终点的链，如果其上面有 $k$ 个红点，那么就意味着它有 $\lceil \frac{|s|-k}2 \rceil$ 个绿点，同时最终连接终点的点一定是绿点。

而对于两条红点数量相同的链，它们对答案的贡献与红点的具体位置无关，因此本质上是一样的，这意味着本质不同的链只有 $\mathcal O(|s|)$ 条。

但我们还要求出有 $k$ 个红点的链的数量。设 $h_{i,l,r}$ 表示从起点走到 $(l,r)$ 对应的节点的路径中，有多少条经过了 $i$ 个红点。那么我们可以采用记忆化搜索的方法 $\mathcal O(|s|^3)$ 求出答案。

现在我们有 $\mathcal O(|s|)$ 条本质不同的链，同时还知道了每条链的数量。至此我们可以对每条链做一次矩阵加速，时间复杂度降为 $\mathcal O(|s|^4 \log (n + |s|))$。

但还不够，我们要想办法建出一个节点数只有 $\mathcal O(|s|)$ 的自动机。构建方法如下（方法来自 CQzhangyu）：

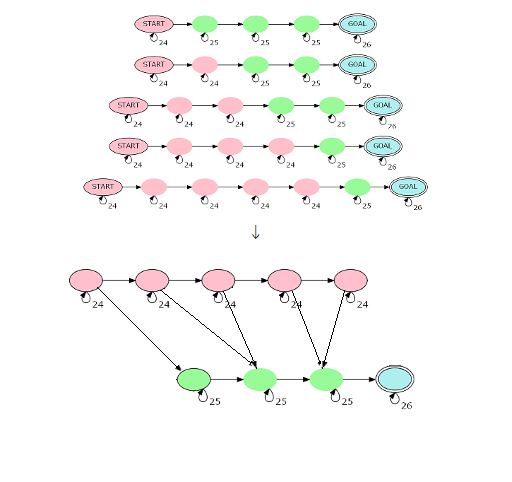
同样的，如果真的理解了上面的转化，肯定能自己根据这样图脑补出来压缩后的自动机具体长成什么样。

压缩后的自动机点数只有 $\mathcal O(|s|)$ 个了，这时候再使用矩阵加速，就可以 $\mathcal O(|s|^3 \log (n+|s|))$。

然而这玩意儿稍微有点卡常，但如果我们把状态转移设计成只能从编号小的往编号大的点转移，那么矩阵乘法时常数可以除以 $6$。

最后还有一个问题，$n+|s|$ 如果为奇数，咋办？

唯一的区别在于，在最后一步的时候，包含两个字符的绿点无法再转移到终点。

那么，我们只保留这样的链，同时去掉终点的自环，这样得到的结果就是要去掉的方案数。

代码

const int N = 207, M = 307;
int n, m, k;
char s[N];
bool v[N][N][N];
modint h[N][N][N], f[M], g[M][M], F[M], G[M][M];

inline modint H(int i, int l, int r) {
    if (i < 0) return 0;
    if (v[i][l][r]) return h[i][l][r];
    v[i][l][r] = 1;
    if (l == 1 && r == m) return h[i][l][r] = !i;
    if (l != 1 && s[l-1] != s[r]) h[i][l][r] += H(i - 1, l - 1, r);
    if (r != m && s[l] != s[r+1]) h[i][l][r] += H(i - 1, l, r + 1);
    if (l != 1 && r != m && s[l-1] == s[r+1]) h[i][l][r] += H(i, l - 1, r + 1);
    return h[i][l][r];
}

inline int ceil(int x) {
    return (x >> 1) + (x & 1);
}

inline void mul(modint f[M], modint g[M][M]) {
    modint a[M];
    for (int j = 1; j <= k; j++)
        for (int i = 1; i <= k; i++)
            a[i] += f[j] * g[j][i];
    for (int i = 1; i <= k; i++) f[i] = a[i];
}

inline void mul(modint g[M][M]) {
    modint a[M][M];
    for (int i = 1; i <= k; i++)
        for (int o = i; o <= k; o++)
            for (int j = o; j <= k; j++)
                a[i][j] += g[i][o] * g[o][j];
    for (int i = 1; i <= k; i++)
        for (int j = 1; j <= k; j++)
            g[i][j] = a[i][j];
}

inline void ksm(int o) {
    while (o) {
        if (o & 1) mul(f, g);
        mul(g), o >>= 1;
    }
}

int main() {
    rds(s, m), rd(n), k = m + ceil(m);
    for (int i = 0; i < m; i++) {
        modint c;
        for (int j = 1; j <= m; j++) {
            c += H(i, j, j);
            if (j != m && s[j] == s[j+1]) c += H(i, j, j + 1);
        }
        if (i) {
            g[i][k-ceil(m-i)] = c, g[i][i] = 24;
            if (i != 1) g[i-1][i] = 1;
            else f[i] = 1;
        } else {
            f[m] = c, g[k][k] = 26;
            for (int j = m; j < k; j++) g[j][j+1] = 1, g[j][j] = 25;
        }
    }
    if ((n + m) & 1) {
        for (int i = 1; i <= k; i++) F[i] = f[i];
        for (int i = 1; i <= k; i++)
            for (int j = 1; j <= k; j++)
                G[i][j] = g[i][j];
    }
    ksm(ceil(n + m));
    if (!((n + m) & 1)) return print(f[k]), 0;
    modint ans = f[k];
    for (int i = 1; i <= k; i++) f[i] = F[i];
    for (int i = 1; i <= k; i++)
        for (int j = 1; j <= k; j++)
            g[i][j] = G[i][j];
    for (int i = 0; i < m; i++) {
        modint c;
        for (int j = 1; j <= m; j++)
            if (j != m && s[j] == s[j+1]) c += H(i, j, j + 1);
        if (i) g[i][k-ceil(m-i)] = c;
        else f[m] = c, g[k][k] = 0;
    }
    ksm(ceil(n + m));
    print(ans - f[k]);
    return 0;
}