AtCoder Grand Contest 027 题解
Visits: 440
Candy Distribution Again
排序后从小到大贪心的选。
const int N = 107;
int n, x, a[N], s;
int main() {
rd(n, x), rda(a, n);
sort(a + 1, a + n + 1);
for (int i = 1; i <= n; s += a[i++])
if (s + a[i] > x) return print(i - 1), 0;
print(n - (s != x));
return 0;
}
Garbage Collector
枚举次数 $k$,注意到从后往前的贡献为 $5,5,7,9,\cdots$,因此贪心地将最后 $k$ 个作为第一个,次后 $k$ 个作为第二个,以此类推。
复杂度是调和级数 $\mathcal O(n \log n)$,另外计算中会爆 long long 但答案不会爆,用 __int128 或者剪枝都可以。
const int N = 2e5 + 7;
int n;
__int128 x, p[N], s[N], d[N], ans = 1e36;
int main() {
rd(n), rd(x), rda(p, n);
for (int i = 1; i <= n; i++) s[i] = s[i-1] + p[i];
d[1] = d[2] = 5;
for (int i = 3; i <= n; i++) d[i] = d[i-1] + 2;
for (int k = 1; k <= n; k++) {
__int128 now = (k + n) * x;
for (int i = n, t = 1; i > 0; i -= k, t++)
now += d[t] * (s[i] - (i - k > 0 ? s[i-k] : 0));
ans = min(ans, now);
}
print(ans);
return 0;
}
ABland Yard
若一条边连接的两个点字符相同,则标为 0,否则标为 1。
那么合法当且仅当存在一个 01 环。
类似拓扑排序,每次删掉一个连边都是同一个字符的点。
如果最后剩下点没被删掉说明存在,否则不存在。
const int N = 2e5 + 7;
int n, m, d[N][2];
char s[N];
vi e[N];
queue<int> q;
bool v[N];
int main() {
rd(n, m), rds(s, n);
for (int i = 1, x, y; i <= m; i++)
rd(x, y), e[x].pb(y), e[y].pb(x), ++d[x][s[y]&1], ++d[y][s[x]&1];
for (int i = 1; i <= n; i++)
if (!d[i][0] || !d[i][1]) q.push(i), v[i] = 1;
while (q.size()) {
int x = q.front();
q.pop();
for (int y : e[x])
if (!v[y] && !--d[y][s[x]&1]) q.push(y), v[y] = 1;
}
for (int i = 1; i <= n; i++)
if (!v[i]) return prints("Yes"), 0;
prints("No");
return 0;
}
Modulo Matrix
题意
- 你要构造一个 $n \times n$ 的矩阵 $a$,满足:
- $a_{i,j} \in [1,10^{15}]$。
- 所有 $a_{i,j}$ 互不相同。
- 对于任意两个相邻的数 $x,y$,$\max(x,y) \bmod \min(x,y)$ 为定值。
- $n \le 500$。
题解
如下图构造:
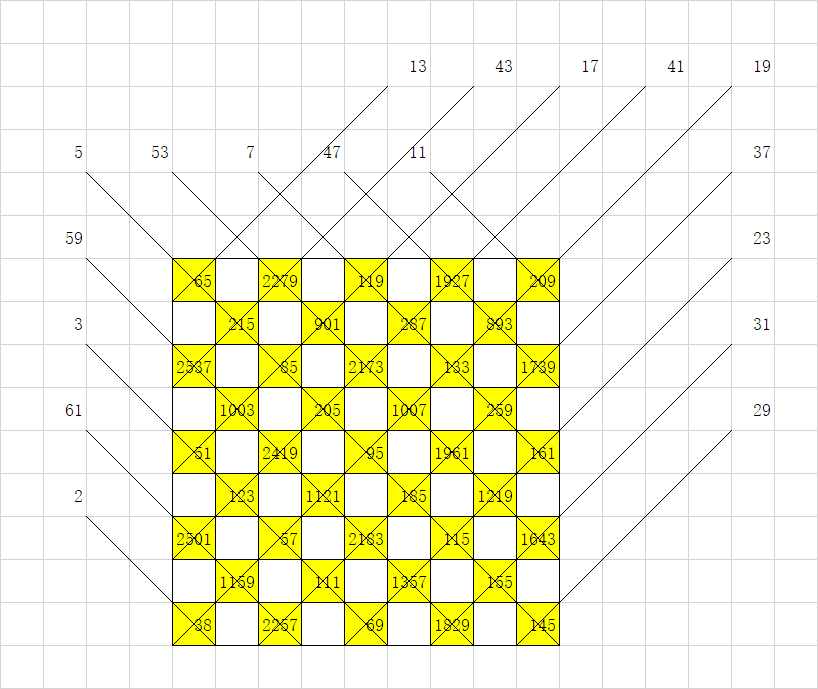
其中黄格子是两个质数的乘积,白格子为周围黄格子的 $\text{lcm} + 1$。
代码
namespace shai {
const int n = 1e6 + 7;
int p[n], v[n], phi[n], miu[n];
inline void init(int n) {
v[1] = phi[1] = miu[1] = 1;
for (int i = 2; i <= n; i++) {
if (!v[i]) p[++p[0]] = v[i] = i, phi[i] = i - 1, miu[i] = -1;
for (int j = 1; j <= p[0] && i * p[j] <= n && p[j] <= v[i]; j++)
v[i*p[j]] = p[j],
phi[i*p[j]] = phi[i] * (p[j] - 1 + (p[j] == v[i])),
miu[i*p[j]] = p[j] == v[i] ? 0 : -miu[i];
}
}
}
using shai::p;
const int N = 507;
int n, a[N], b[N];
int main() {
shai::init(1e4);
rd(n);
for (int i = 1; i <= n; i++) a[i] = p[i&1?i/2+1:n*2-i/2+1];
for (int i = 1; i <= n; i++) b[i] = p[(i&1?n-i/2:n+i/2)+(n&1)];
a[0] = a[n+1] = b[0] = b[n+1] = 1;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
print((i ^ j) & 1 ? 1ll * a[(i+j)/2] * a[(i+j)/2+1] * b[(n+i-j+(n&1))/2] * b[(n+i-j+(n&1))/2+1] + 1 : 1ll * a[(i+j)/2] * b[(n+i-j+(n&1))/2], " \n"[j==n]);
return 0;
}
ABBreviate
题意
- 给定一个仅包含
ab的字符串 $s$。 - 你会进行若干次操作,每次操作可以将 $s$ 中的一个
aa替换成b,或将一个bb替换成a。 - 求能够生成的字符串数量。
- $|s| \le 10^5$,答案对 $10^9+7$ 取模。
题解
首先如果没有 aa 或 bb,答案为 $1$。
否则,令 a 为 $2$,b 为 $1$,可以发现每次操作都不影响和 $\bmod 3$ 的值。
考虑到如果一个 $t$ 能被 $s$ 生成,那么必然是 $t$ 中的每个字符对应 $s$ 中的某一段,且这两段的和 $\bmod 3$ 的值相同。
可以证明从前往后贪心匹配 $t$ 中的每个字符,如果最后 $s$ 剩下的部分之和 $\bmod 3 = 0$,则 $t$ 合法。
于是可以简单的 $\mathcal O(n)$ DP 求出答案了。
代码
const int N = 1e5 + 7;
int n, a[N], p[N][3];
char s[N];
modint f[N], ans;
inline bool pd() {
for (int i = 1; i < n; i++)
if (s[i] == s[i+1]) return 0;
return 1;
}
int main() {
rds(s, n);
if (pd()) return print(1), 0;
for (int i = 1; i <= n; i++) a[i] = (a[i-1] + (s[i] & 1) + 1) % 3;
for (int i = 0; i < 3; i++) p[n+1][i] = n + 1;
for (int i = n; i; i--) {
for (int j = 0; j < 3; j++) p[i][j] = p[i+1][j];
p[i][a[i]] = i;
}
f[0] = 1;
for (int i = 0; i <= n; i++) {
if (i && a[i] == a[n]) ans += f[i];
for (int j = 1; j < 3; j++)
f[p[i+1][(a[i]+j)%3]] += f[i];
}
print(ans);
return 0;
}
Grafting
题意
- 给定两棵 $n$ 个点的树 $A,B$。
- 一开始 $A$ 的所有点都是白色,你可以对 $A$ 进行若干次下列操作使得 $A$ 与 $B$ 相同:
- 选择一个白色的叶子节点 $x$。
- 删掉与 $x$ 相连的边。
- 加上一条连接 $x$ 与另一个节点 $y$ 的边。
- 将 $x$ 染成黑色。
- 判断是否可行,如果可行,请最小化操作步数。
- $n \le 50$,多组数据组数 $T \le 20$。
题解
首先判一下 $A,B$ 是否本身就相同,如果是就直接输出 $0$。
否则枚举第一次操作的 $x,y$,然后以 $x$ 为根把两棵树拎起来(其中 $A$ 是操作后的树)。
那么某个节点会被修改当且仅当这个点在两棵树上的父亲不同。
另外可以得到一些约束条件:
- 若某个点不需要被修改,这意味着它在 $A$ 上的父亲不可能成为叶子,因此若它在 $A$ 上的父亲需要被修改,那么无解。
- 在 $A$ 中,一个点一定比它的父亲先被修改(如果都要被修改的话)。
- 在 $B$ 中,一个点一定比它的父亲后被修改(如果都要被修改的话)。
根据后两个条件我们可以得到一个有向图,如果这个有向图无环则说明有解,否则无解。
时间复杂度 $\mathcal O(Tn^3)$。
代码
const int N = 57, inf = 1e9;
int n, f[2][N], d[N];
vi e[2][N], g[N];
bool v[N];
queue<int> q;
inline bool pd0() {
for (int i = 1; i <= n; i++)
if (e[0][i] != e[1][i]) return 0;
return 1;
}
inline void change(int x, int y, int z) {
e[0][x][0] = z;
for (int &o : e[0][y])
if (o == x) {
swap(o, e[0][y].back());
break;
}
e[0][y].pop_back(), e[0][z].pb(x);
}
void dfs(int o, int x, int fa) {
f[o][x] = fa;
for (int y : e[o][x])
if (y != fa) dfs(o, y, x);
}
inline void add(int x, int y) {
g[x].pb(y), ++d[y];
}
inline int calc(int x, int y) {
int z = e[0][x][0], now = y != z;
change(x, z, y);
dfs(0, x, 0), dfs(1, x, 0);
change(x, y, z);
for (int i = 1; i <= n; i++)
now += v[i] = f[0][i] != f[1][i], g[i].clear(), d[i] = 0;
for (int i = 1; i <= n; i++)
if (!v[i] && v[f[0][i]]) return inf;
for (int o = 0; o < 2; o++)
for (int i = 1; i <= n; i++)
if (v[i] && v[f[o][i]])
add(o ? f[o][i] : i, o ? i : f[o][i]);
for (int i = 1; i <= n; i++)
if (v[i] && !d[i]) q.push(i);
while (q.size()) {
int x = q.front();
q.pop(), v[x] = 0;
for (int y : g[x])
if (!--d[y]) q.push(y);
}
for (int i = 1; i <= n; i++)
if (v[i]) return inf;
return now;
}
inline void solve() {
rd(n);
for (int o = 0; o < 2; o++) {
for (int i = 1; i <= n; i++) e[o][i].clear();
for (int i = 1, x, y; i < n; i++)
rd(x, y), e[o][x].pb(y), e[o][y].pb(x);
for (int i = 1; i <= n; i++)
sort(e[o][i].begin(), e[o][i].end());
}
if (pd0()) return print(0);
int ans = inf;
for (int x = 1; x <= n; x++)
if (e[0][x].size() == 1u)
for (int y = 1; y <= n; y++)
ans = min(ans, calc(x, y));
print(ans == inf ? -1 : ans);
}
int main() {
int T;
rd(T);
while (T--) solve();
return 0;
}


