模拟退火 学习笔记
Visits: 536
又是个之前学过现在忘光了的算法。。。
简介
模拟退火是一种随机化算法,在优化型题目(选手得分依赖于其输出结果与最优解的比较)中非常有用,而这类题目通常为提交答案题。
使用条件
- 方案的数量极大甚至无穷大,无法方便地得到最优解。
- 方案的优劣程度并不是一个单峰函数,如果是单峰函数那么显然有更简单的方法。
- 两个方案的优劣程度与两个方案的相似程度有关,换句话说,我们有可能从一个较优解推出另一个较优解。
大致流程
- 首先随机出一个解。
- 然后不断根据当前最优解生成一个相似的新解。
- 如果新解比当前最优解更优,则用新解替换当前最优解;否则,以一定概率替换当前最优解。
- 最后取所有随机到的解中最优的为答案。
流程细节
大致流程中,当根据当前最优解生成的新解比当前最优解劣时,以一定概率替换当前最优解,这里的概率如何计算呢?
考虑物理中的退火过程,退火即降温。起初温度很高,然后不断进行降温,在温度越高时概率越大,越低时概率越小。
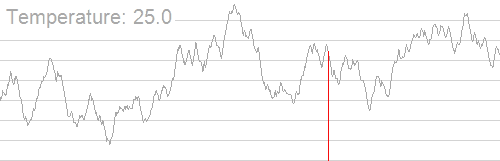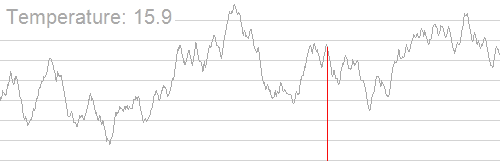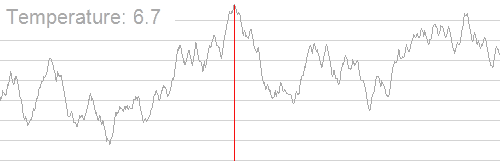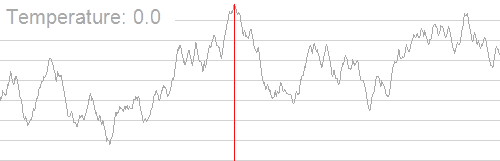
同时,这个概率显然也要跟新旧解之间优劣程度的差相关,差越大概率越小,差越小概率越大。
实现
定义当前温度为 $T$,新解与当前最优解之间优劣程度之差为 $E(\le 0)$,则用新解替换当前最优解的概率为:
$$
e^{\frac{E}{T}}
$$
这个概率符合上面我们的两个要求,判断时将其与一个 $[0,1]$ 内随机的数比较,如果这个概率更大,则替换,否则不替换。
如何进行降温呢?
首先要设三个正实参数:初始温度 $T_0$,降温系数 $delta$,终止温度 $T_k$。其中 $T_0$ 较大,$delta < 1$ 但是很接近 $1$,$T_k > 0$ 但很接近 $0$。
一开始 $T \leftarrow T_0$,随后每次生成新解后 $T \leftarrow delta \cdot T$,当 $T < T_k$ 时结束。
另外,根据当前最优解生成新解时,也可以将 $T$ 纳入参考中,即 $T$ 越小生成的新解越相似。
优化
首先可以想到的是,多次进行模拟退火取最优解。
显然模拟退火的次数越多,消耗的时间越长,得到的答案越优。
在提交答案题中,我们可以跑一整场比赛都不要紧。
但是在传统题中,时间限制的存在让我们无法这么做,于是我们要尽可能的利用更多的时间去计算,同时不能超时。
考虑卡时,即最大化程序运行时间。clock() 函数返回程序运行时间,因此我们可以通过 while (1.0 * clock() / CLOCKS_PER_SEC < time_limit - eps) 进行卡时。
参考资料
- OI Wiki 模拟退火


